Una permutación es una combinación en donde el orden es importante. La
notación para permutaciones es P(n,r) que es la cantidad de permutaciones de
“n” elementos si solamente se seleccionan “r”
.
Ejemplo: Si nueve estudiantes toman un examen y
todos obtienen diferente calificación, cualquier alumno podría alcanzar la
calificación más alta. La segunda calificación más alta podría ser obtenida por
uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de
los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504
combinaciones posibles de las tres calificaciones más alta.


Hay dos tipos de permutaciones:
- Se permite repetir: como la cerradura de arriba, podría ser "333".
- Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.
1. Permutaciones con repetición
Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:
n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)
Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1000 permutaciones
Así que la fórmula es simplemente:
| nr |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa) |
2. Permutaciones sin repetición
En este caso, se reduce el número de opciones en cada paso.
 |
Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar?
Después de elegir por ejemplo la "14" no puedes elegirla otra vez.
|
Así que tu primera elección tiene 16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14, 13, etc. Y el total de permutaciones sería:
16 × 15 × 14 × 13 ... = 20,922,789,888,000
Pero a lo mejor no quieres elegirlas todas, sólo 3 de ellas, así que sería solamente:
16 × 15 × 14 = 3360
Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.
¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
 |
La función factorial (símbolo: !) significa que se multiplican números descendentes. Ejemplos:
|
| Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones. | |
Así que si quieres elegir todas las bolas de billar las permutaciones serían:
16! = 20,922,789,888,000
Pero si sólo quieres elegir 3, tienes que dejar de multiplicar después de 14. ¿Cómo lo escribimos? Hay un buen truco... dividimos entre 13!...
16 × 15 × 14 × 13 × 12 ...
| = 16 × 15 × 14 = 3360 | |
13 × 12 ...
|
¿Lo ves? 16! / 13! = 16 × 15 × 14
La fórmula se escribe:
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden importa) |
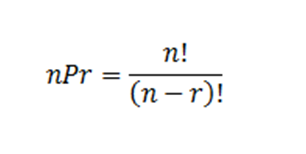
No hay comentarios.:
Publicar un comentario